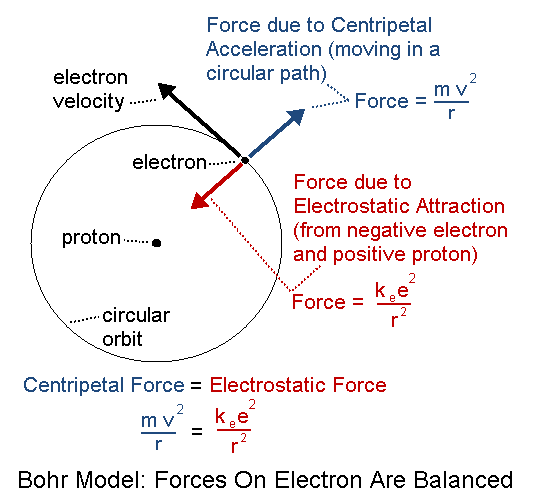
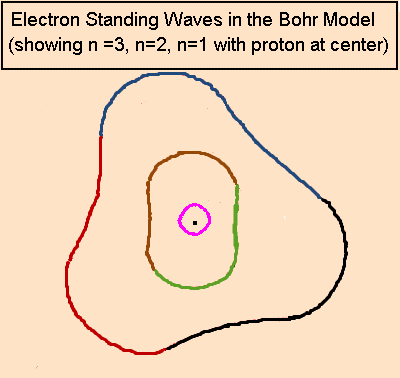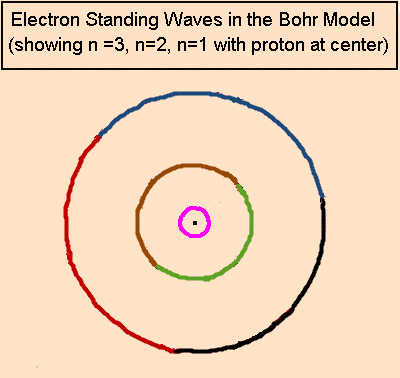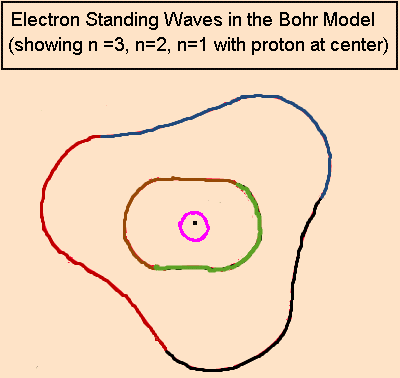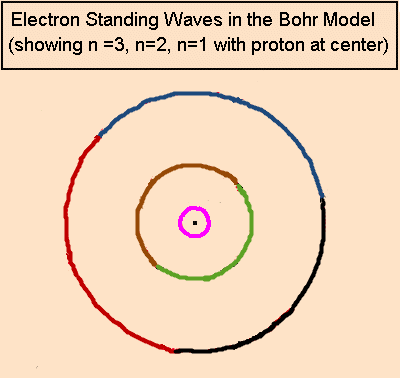
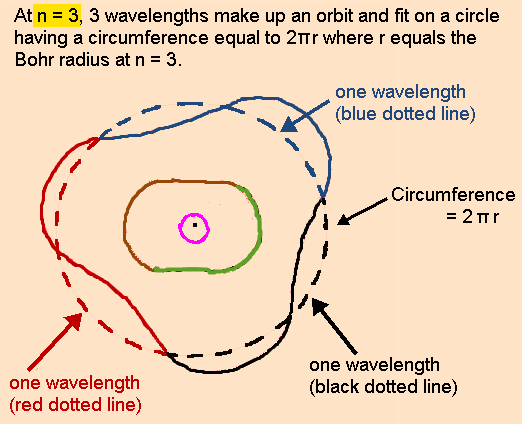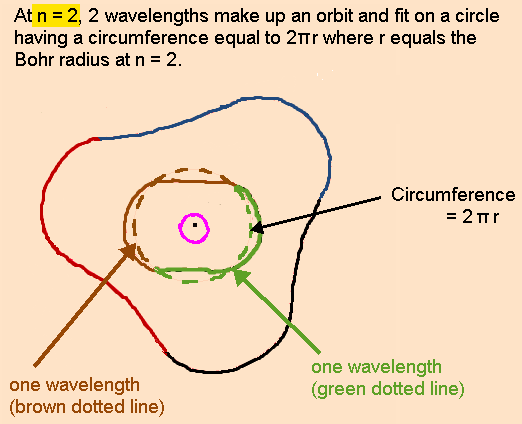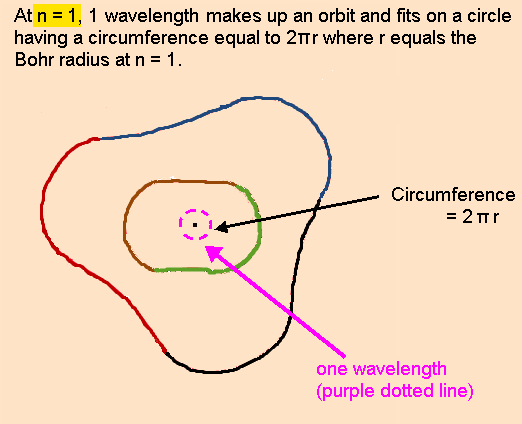
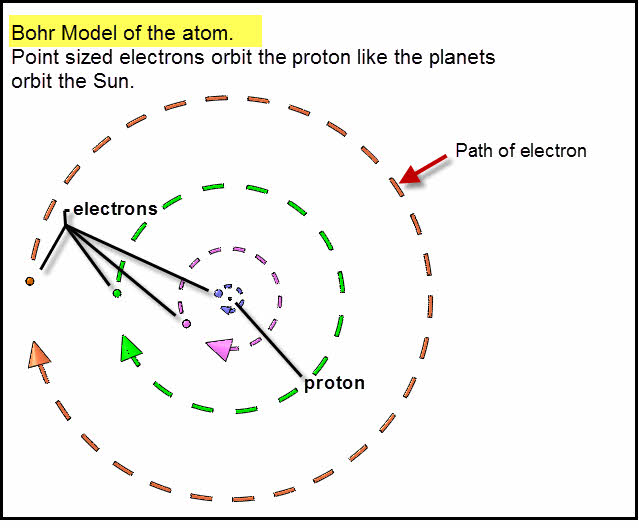
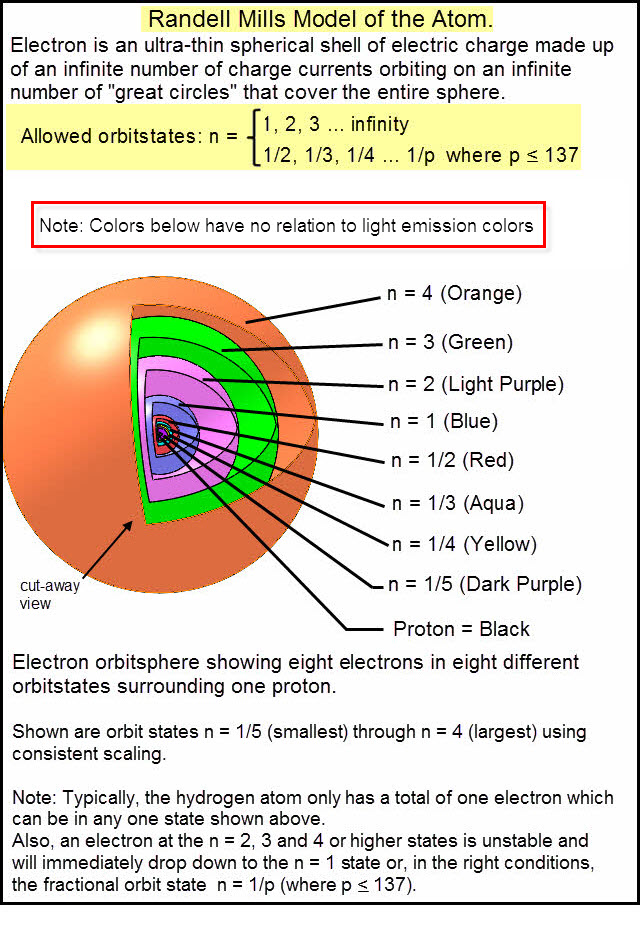
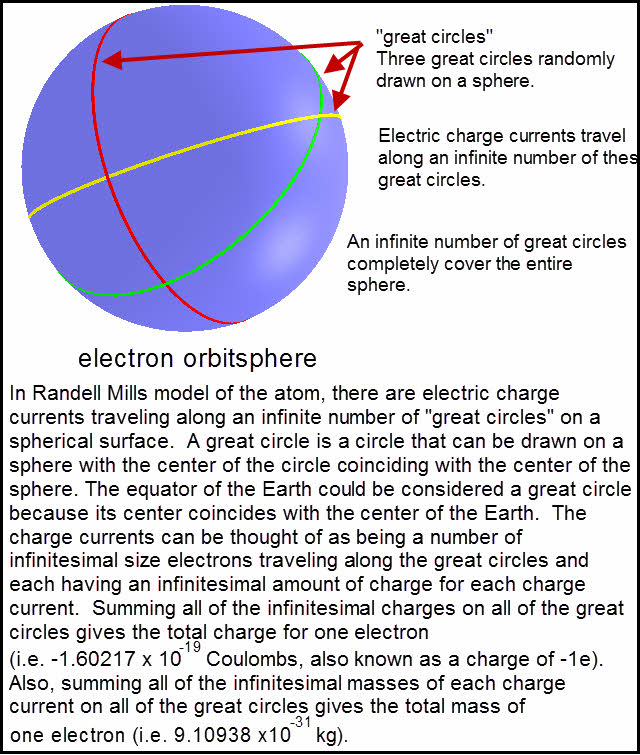
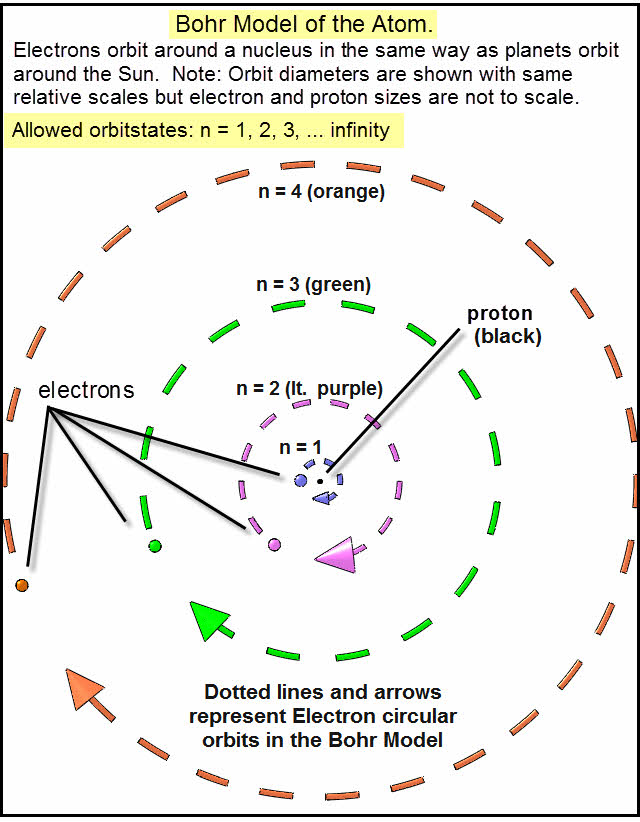
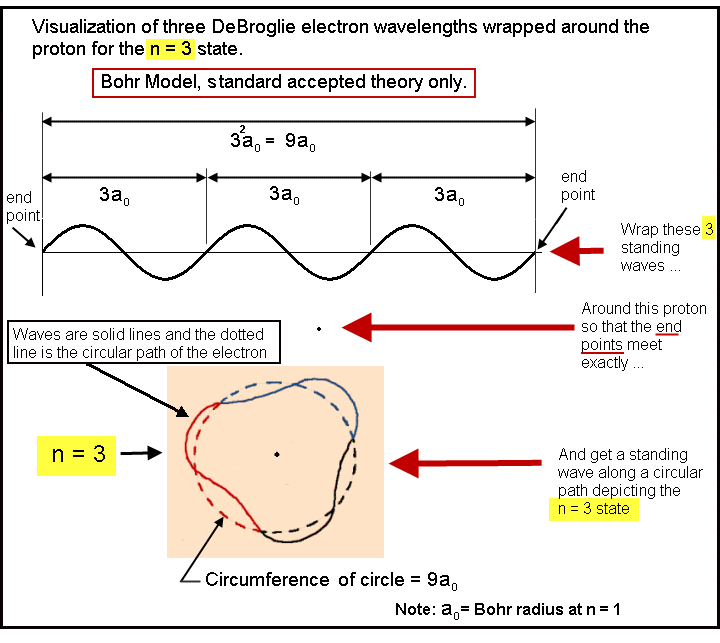
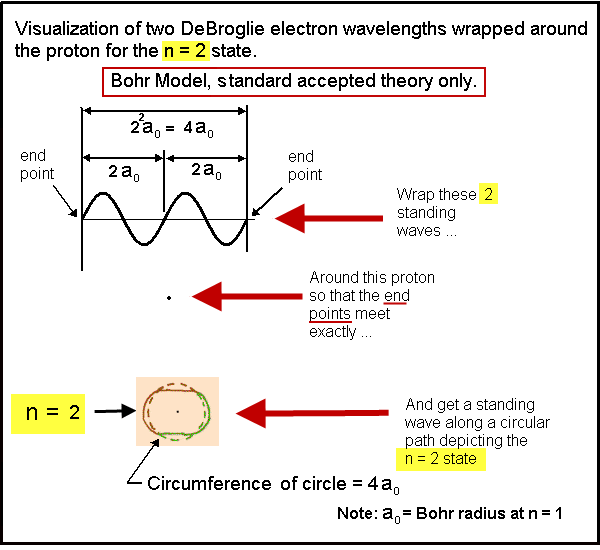
Understanding the Bohr Model first makes it much easier to understand Mills’s model of the atom.
Here are additional resources for understanding the Bohr atom.
Hyperphysics http://hyperphysics.phy-astr.gsu.edu/hbase/bohr.html#c4
Wikipedia http://en.wikipedia.org/wiki/Bohr_model


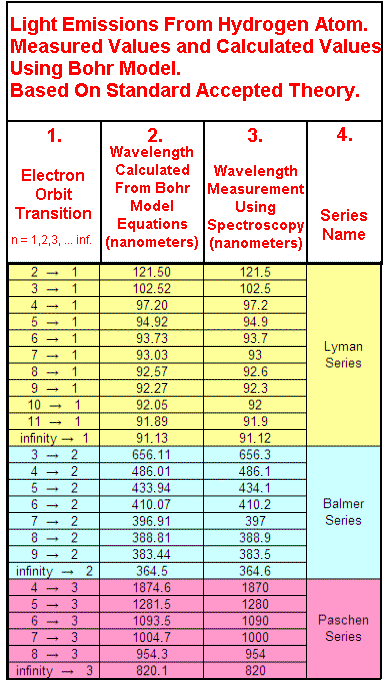
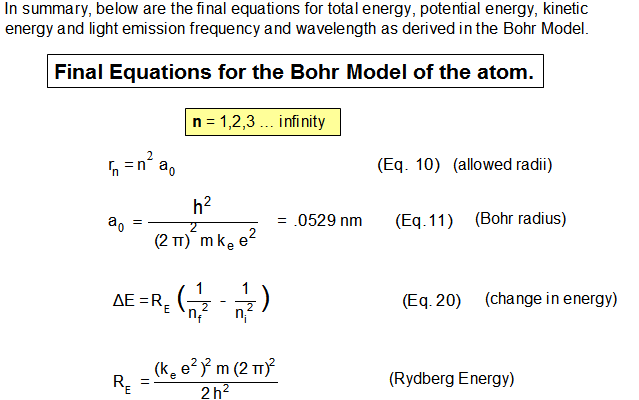
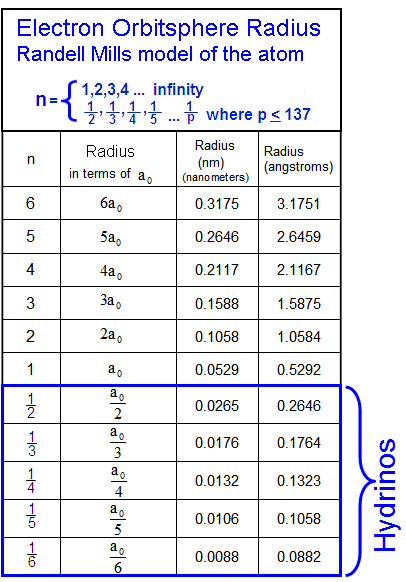
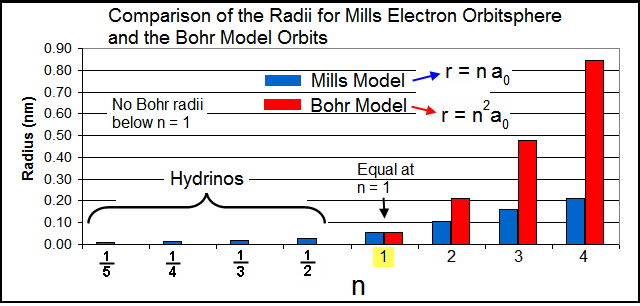
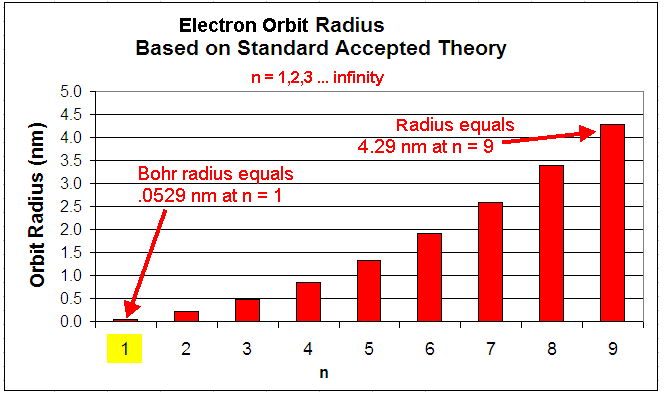
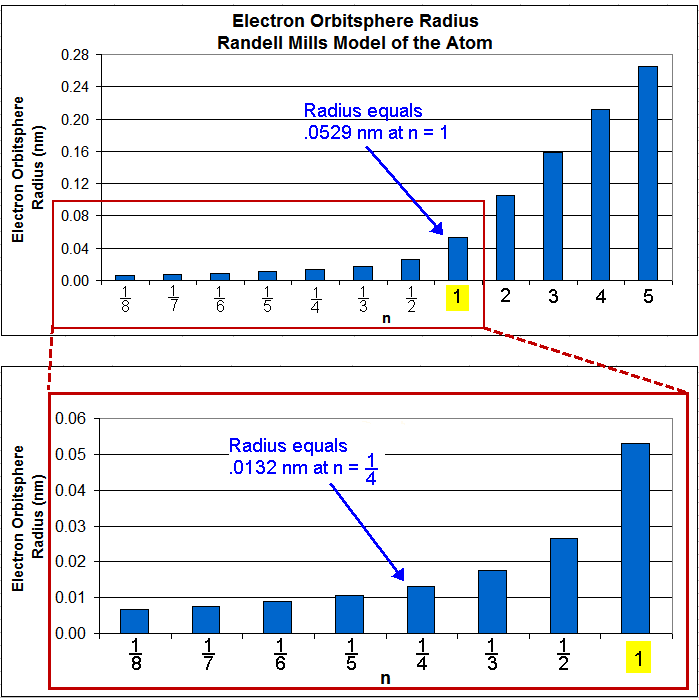
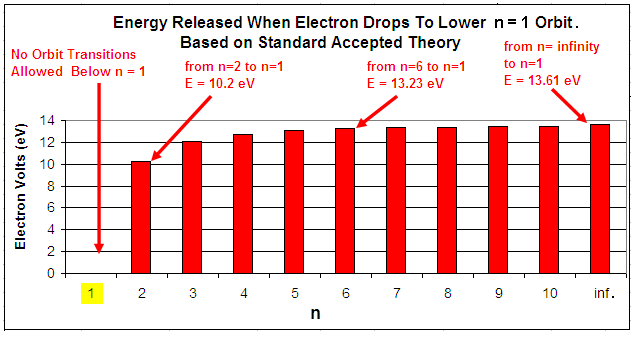
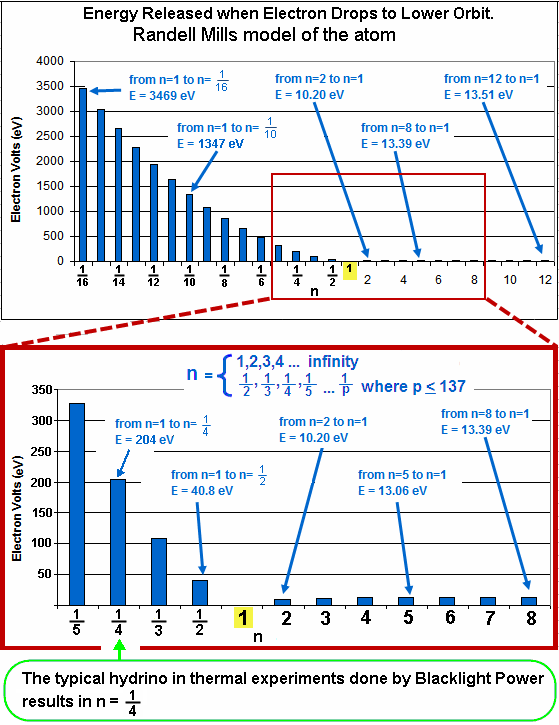
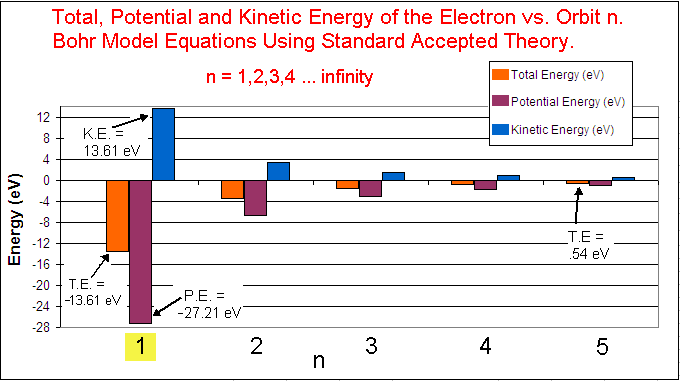
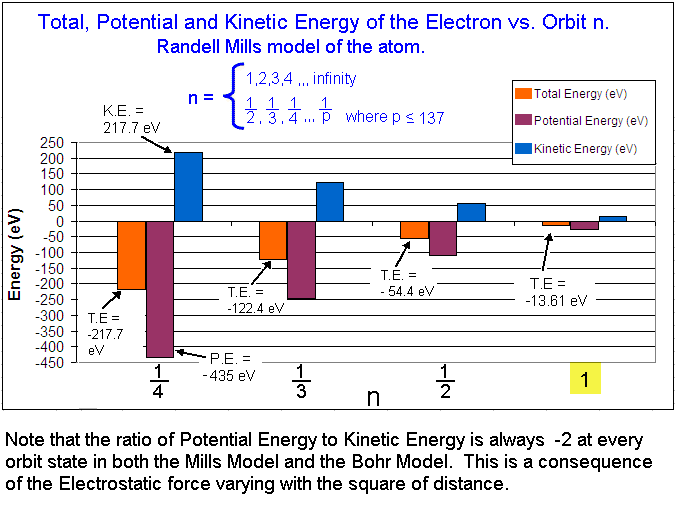
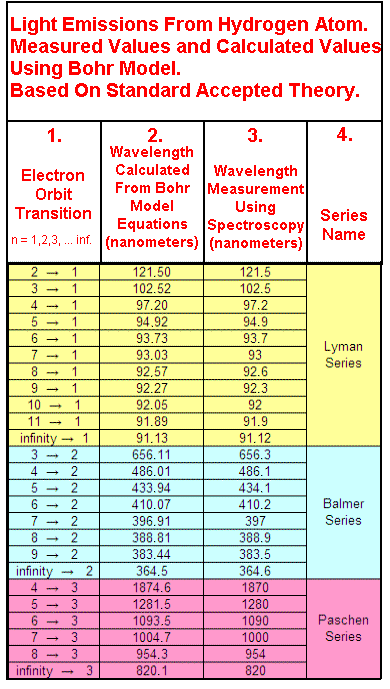
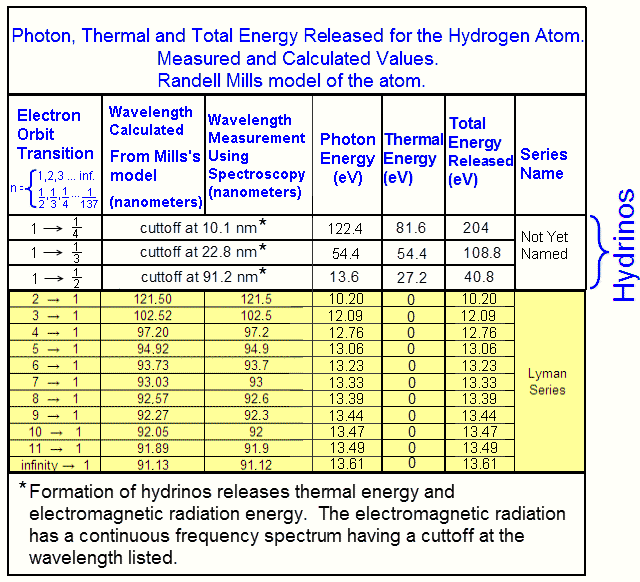
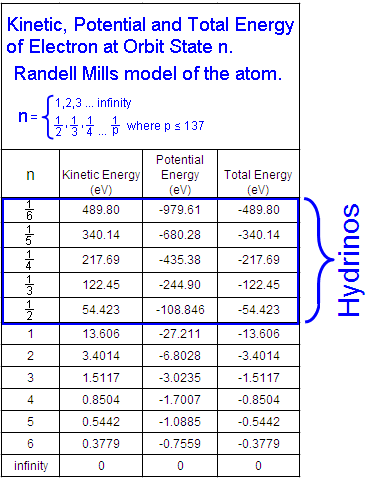
Tables and Graphs.








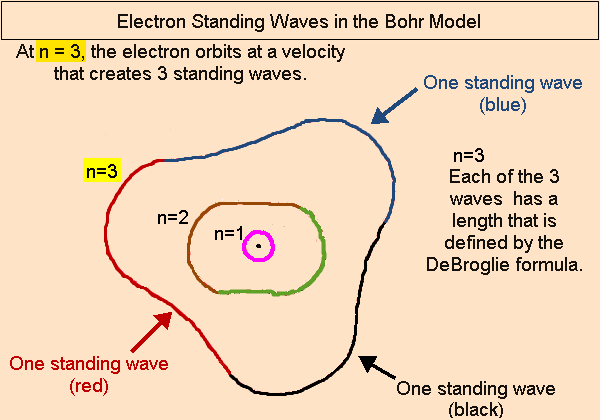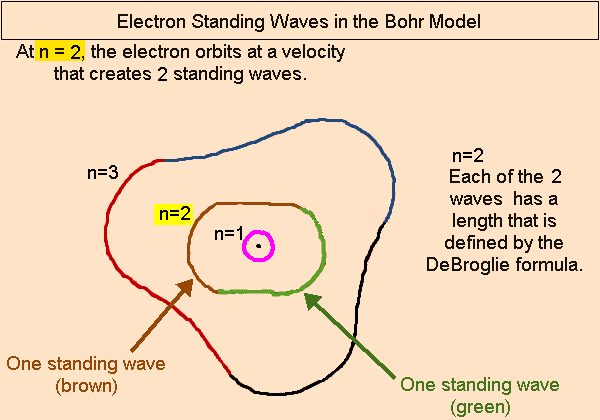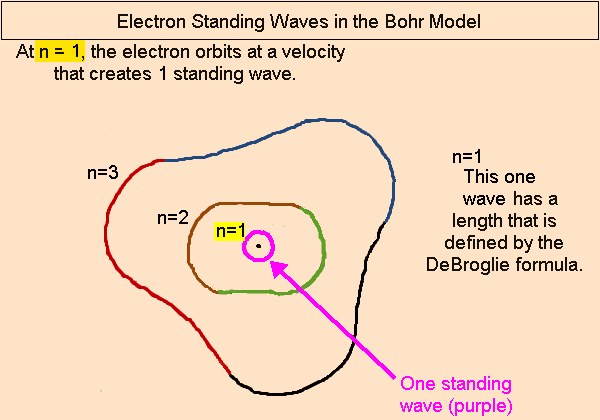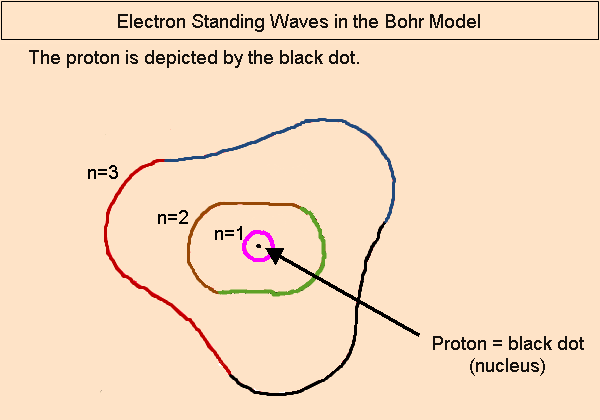
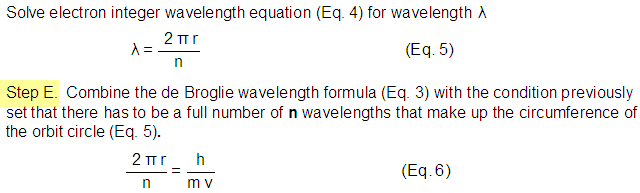






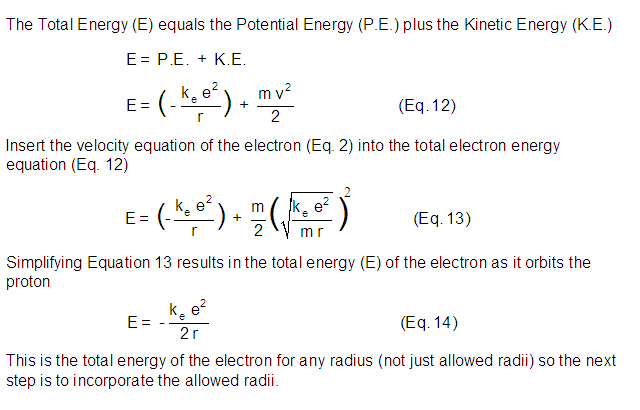
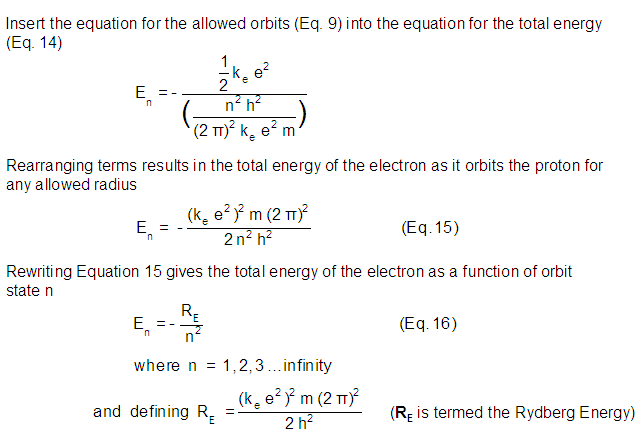






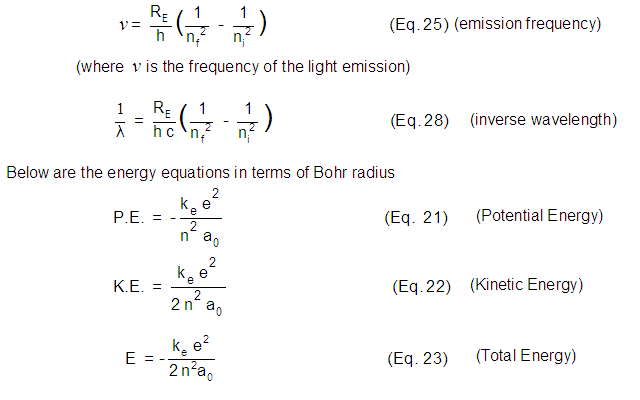
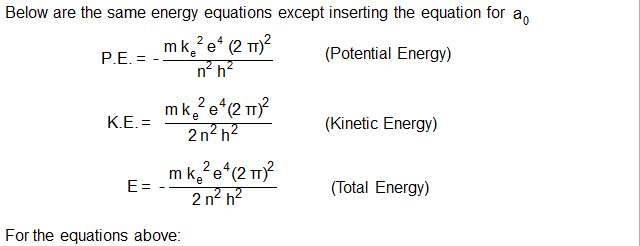






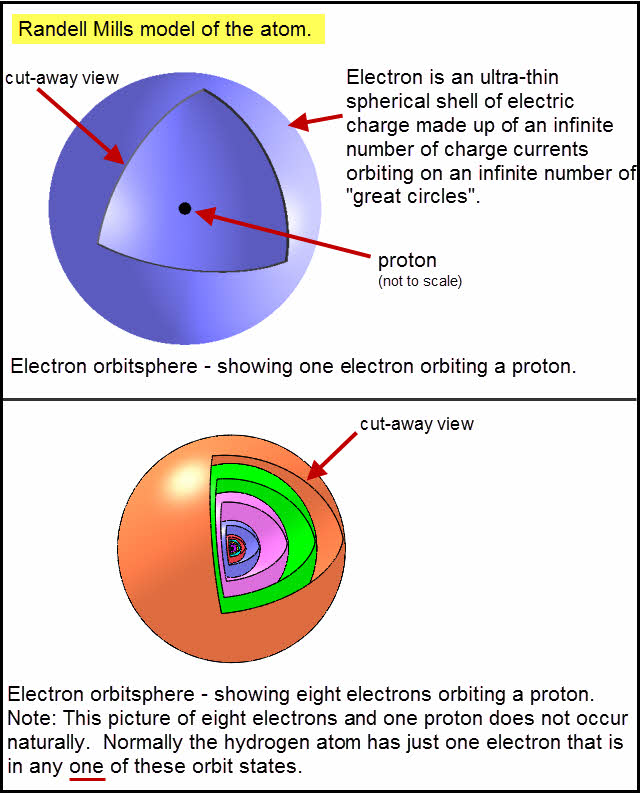
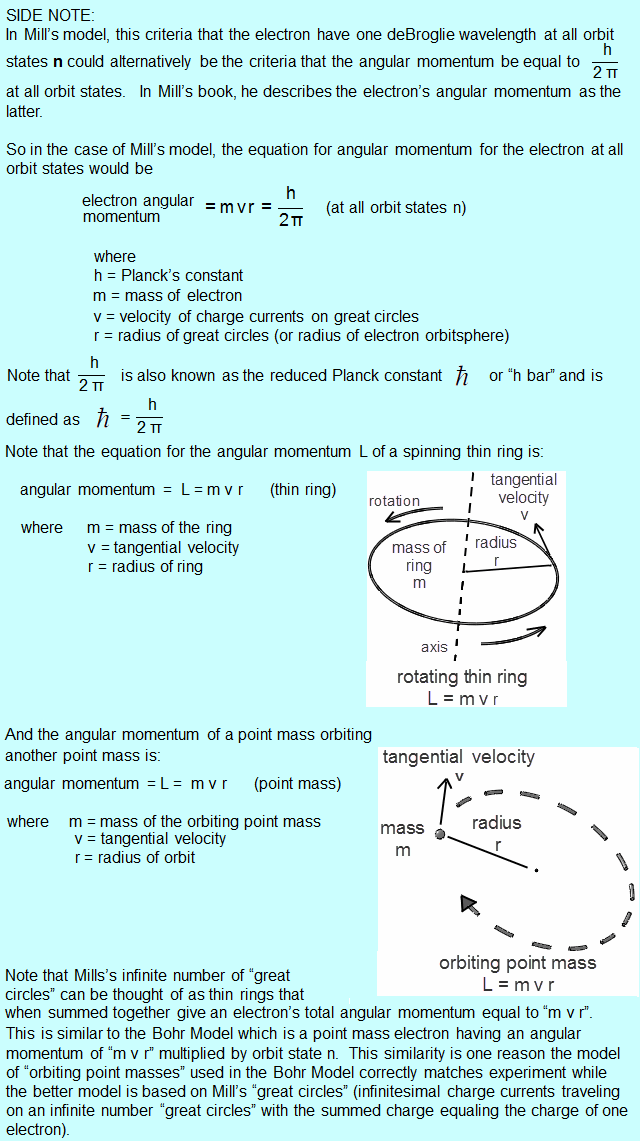





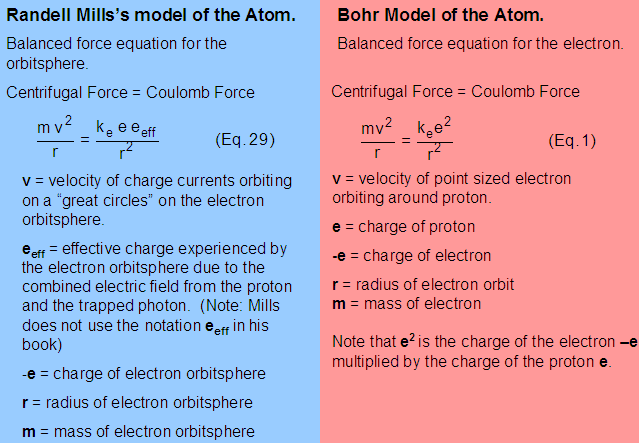




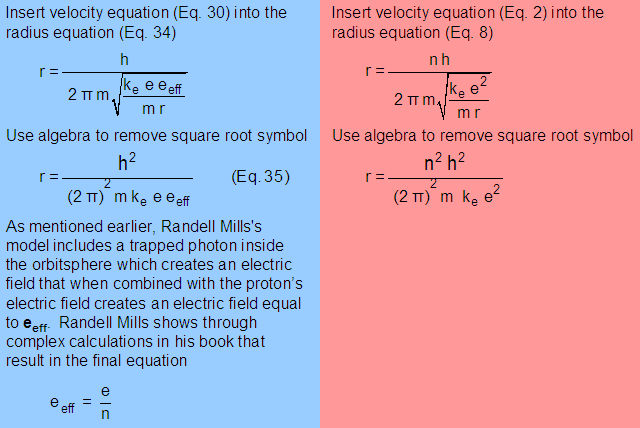











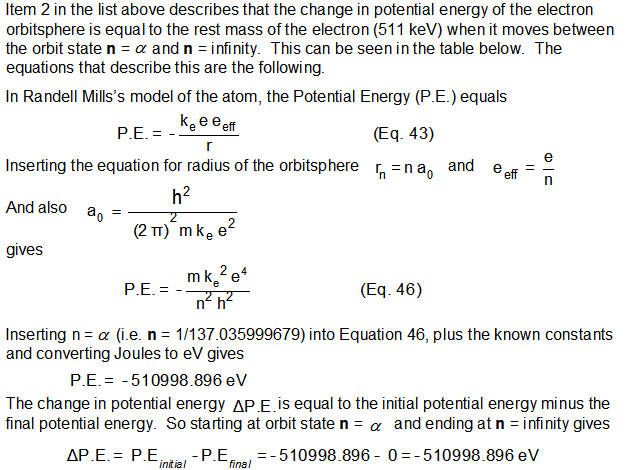

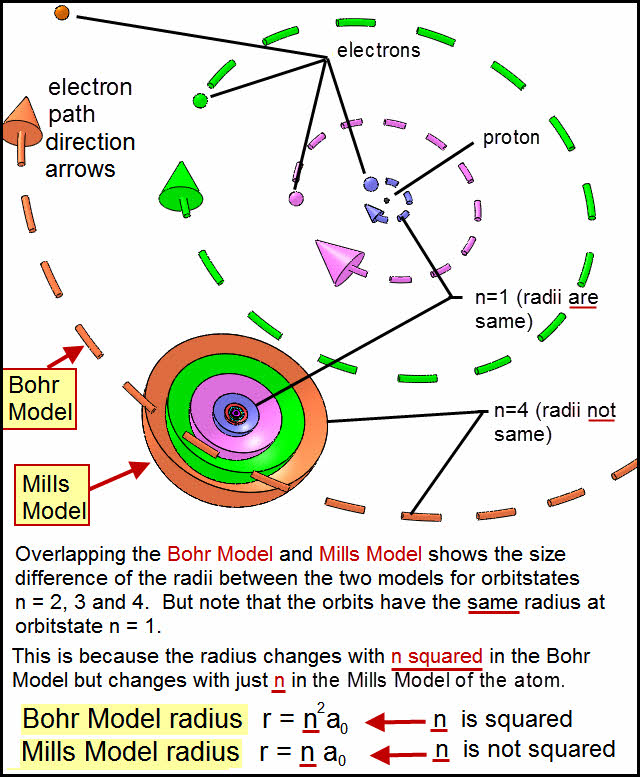
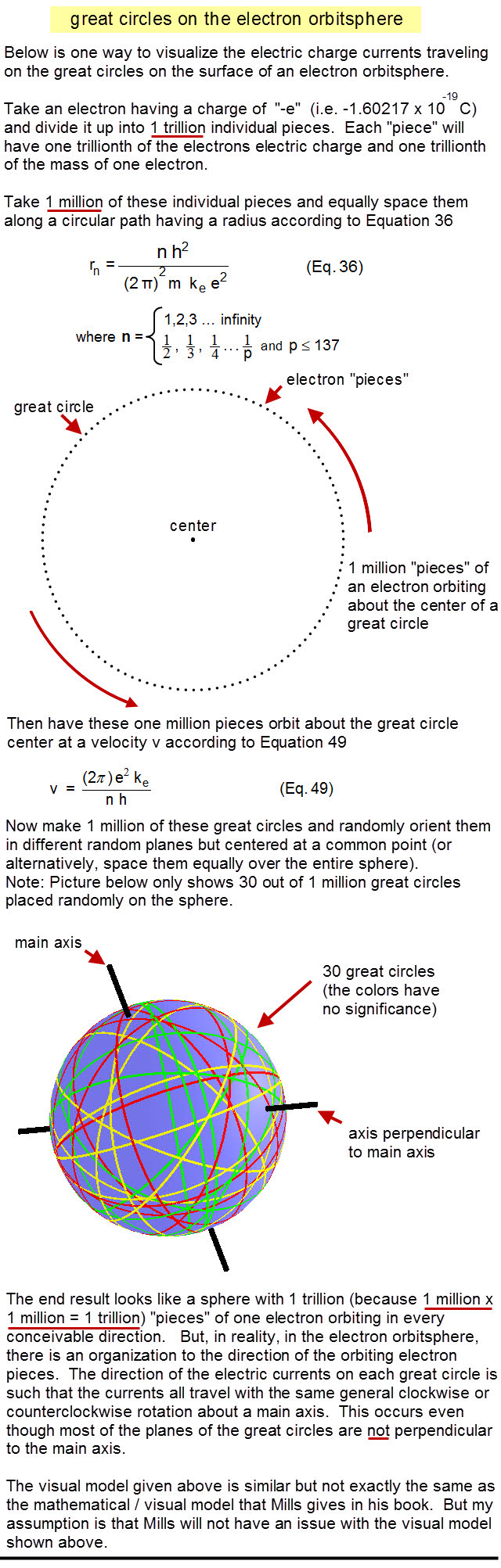
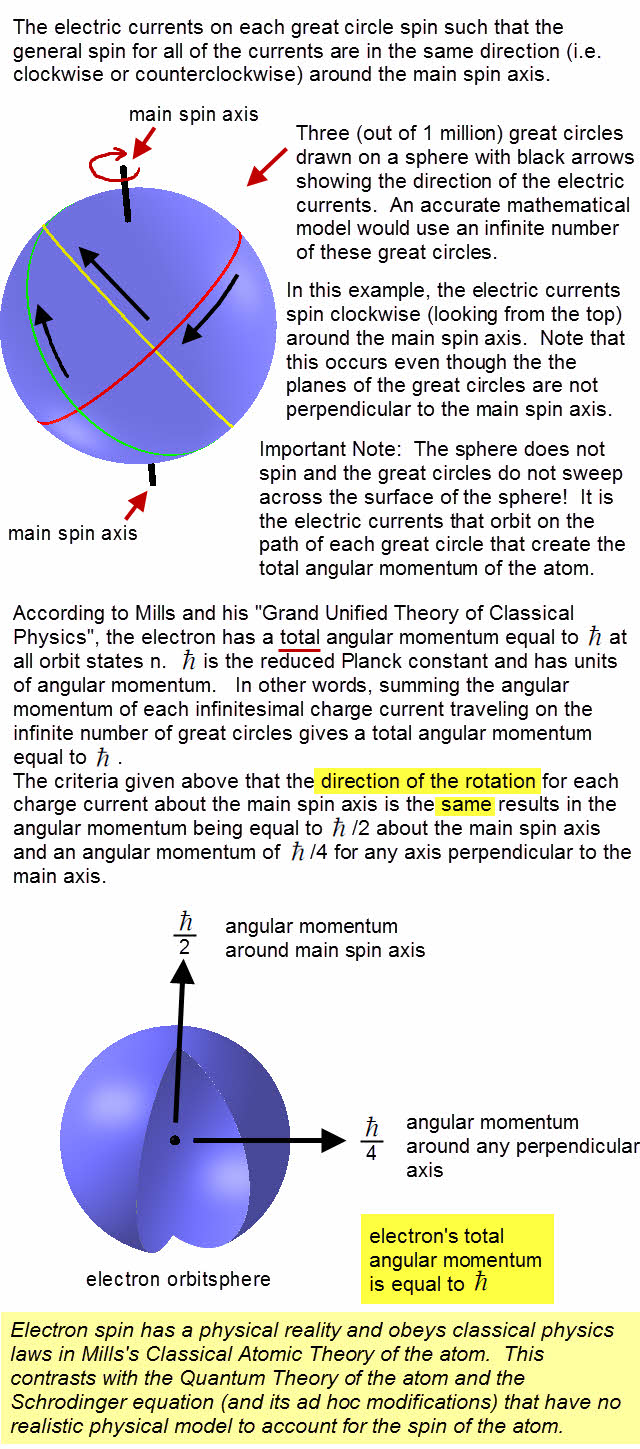
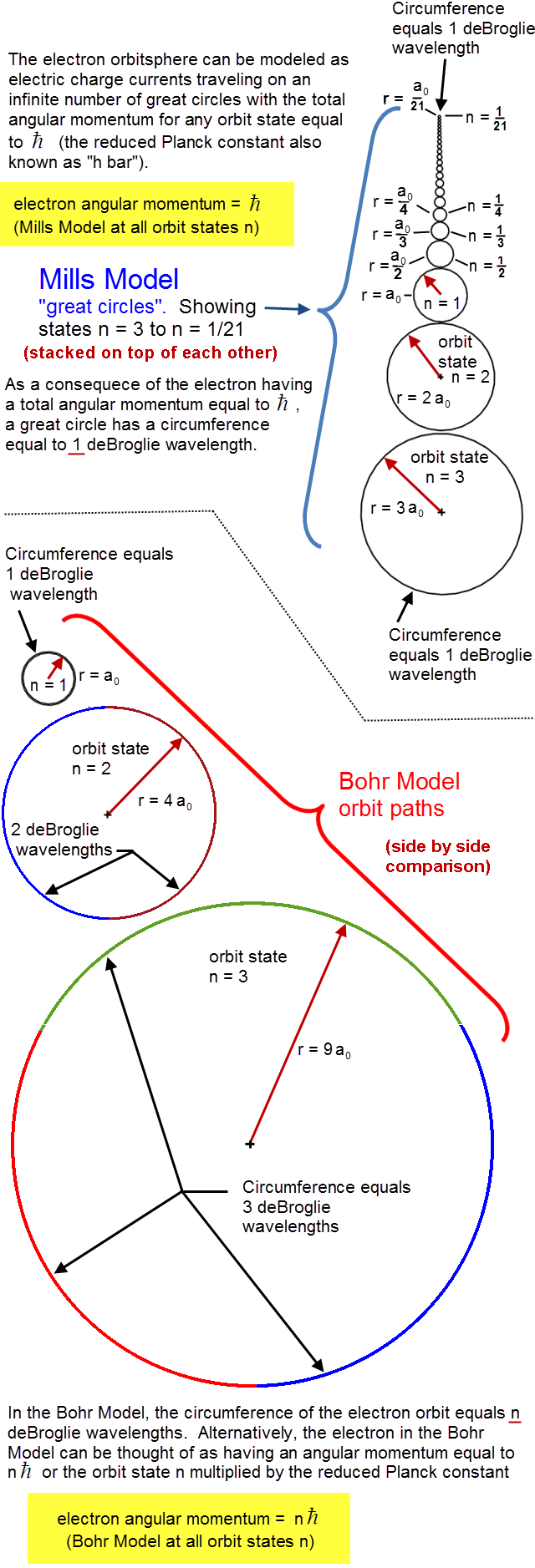











Pingback: home page |